
Mathématiques et Athlétisme : vers de nouveaux sommets olympiques ?
Optimiser les modèles de pistes d’athlétisme pour battre des records au 200m.
En cette difficile période de confinement et d'interdiction de sports collectifs, et à la suite de l’annonce du report des Jeux Olympiques de Tokyo, Amandine Aftalion (Directrice de recherche CNRS, Centre d'Analyse et de Mathématique Sociales de l’EHESS) et Emmanuel Trélat (Professeur Sorbonne Université, directeur du Laboratoire Jacques-Louis Lions; LJLL, Sorbonne Université/Université de Paris/CNRS) continuent de faire courir des champions virtuels. Les deux chercheurs font appel à la modélisation géométrique et aux équations différentielles pour répondre à un défi que nous pose l’application des sciences mathématiques au domaine du sport de haut niveau : serait-il possible de battre des records vieux de 10 et 30 ans en optimisant nos modèles de pistes?
Un nouveau modèle pour un nouveau record du monde
Dans un article qui vient de paraître dans la prestigieuse revue Royal Society Open Science, Amandine Aftalion (DR CNRS) et Emmanuel Trélat (Professeur Sorbonne Université) ont mis au point un modèle mathématique de coureur, qui reproduit fidèlement les performances des champions. Les deux chercheurs montrent qu'il est possible d'optimiser la forme actuelle d'un stade, que les actuels records au 200m peuvent être battus, et que les mathématiques sont omniprésentes et peuvent résoudre des problèmes très divers relevant de toutes les disciplines.
L’épreuve des 200m : le « stadion » des sprinters
En 1894, dans un amphithéâtre de la Sorbonne, le Comité International Olympique a vu le jour. En instituant les Jeux Olympiques, le rêve de Pierre de Coubertin de faire vivre l’héritage d’Olympie s’est concrétisé durant l’époque moderne. L’athlétisme, un des sports les plus anciens au monde, figurait aux programme de la première édition des JO (Athènes, 1896), parmi neuf sports représentés. L’épreuve des 200 mètres du « sport roi » des Olympiades, quant à elle, fut intégrée au programme olympique à partir de 1900 pour les hommes et 1948 pour les femmes(1).
Une des plus anciennes compétitions de course à pied, elle est connue également sous le nom de « stadion » (en référence à la longueur de stade, une course qui se courait en ligne droite et sans virage dans l’antiquité). Le 200m consiste aujourd’hui en un tour de piste avec virages. Son coureur, nullement confronté à la solitude du coureur de fond d’un Spartathlon2, doit néanmoins gagner en vitesse et technique et doser sa force pour faire face à la force centrifuge d’un virage qui s’accroit selon son positionnement de couloir (une force importante voire même entravante pour les couloirs intérieurs par rapport aux couloirs extérieurs pour les pistes à anses de panier conçues pour les stades multisports et présentant des virages à courbure plus grande3).
Le modèle de contrôle optimal
Le modèle mathématique développé couple la mécanique et l'énergie du coureur, notamment sa consommation maximale d'oxygène (VO2 max) et son stock d'énergie anaérobie, en les faisant intervenir dans un système d'équations différentielles reliant la vitesse, l'accélération, la force de propulsion, le contrôle moteur et la motivation du coureur, ce qui permet de déterminer, à travers les coûts et les bénéfices, la meilleure stratégie de course.
Les chercheurs étaient capables de prédire l'évolution des performances de coureurs en fonction de la géométrie optimale d’une piste. Pour répondre au double défi de battre des records et minimiser l'inconvénient des couloirs intérieurs, les chercheurs préconisent une optimisation géométrique basée sur des lignes droites plus courtes et des rayons plus grands, et ce en basant sur le problème du contrôle optimal dit problème du chemin de Dubins4. Cette optimisation est mise en œuvre par la combinaison de logiciels de différenciation automatique et d’optimisation numérique.
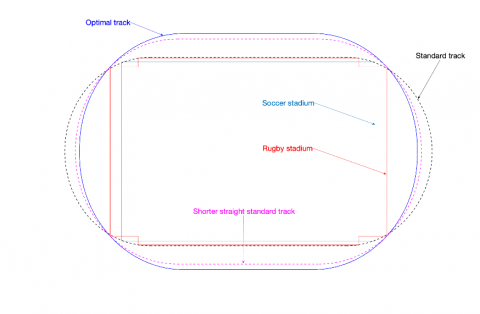
En vert : piste optimale déterminé par ce nouveau modèle. En rose : la piste standard avec une ligne droite raccourcie. En noir : la piste standard classique. © Amandine Aftalion, chercheuse du CNRS au Centre d'analyse et de mathématique sociales (CNRS/EHESS), et Emmanuel Trélat, chercheur de Sorbonne Université au Laboratoire Jacques-Louis Lions (CNRS/Sorbonne Université/ Université de Paris)
« Il y a un temps et un lieu pour une performance réussie »(5)
En analysant la performance de l’américain Michael Johnson à Atlanta en 1996, les chercheurs prouvent, dans le cadre de leurs hypothèses de simulation, qu'il y a gain de temps sur les pistes à géométrie optimisée selon les différents scénarios topologiques, une raison de plus pour nos chercheurs ainsi que tous nos futurs porteurs et porteuses de flamme olympique de continuer à porter ce projet afin d’offrir une fête pour les yeux et les tribunes lors des compétitions à venir.
(1) 200 Metres, World Athletics.
(2) L’épreuve vise à reprendre les mêmes conditions géographiques et saisonnières que l’historique marathon. La course retrace le parcours de Phidippidès, un messager grec envoyé à Sparte en -490 avant J-C, et qui aurait couru de la ville de Marathon jusqu'à Athènes pour annoncer la victoire des Grecs lors de la bataille de Marathon.
(3) Un des trois modèles de pistes certifiées par les fédérations d’athlétismes et réexaminés par les deux scientifiques.
(4) En géométrie, le terme "chemin de Dubins" désigne généralement la courbe la plus courte qui relie deux points situés dans le plan Euclidien bidimensionnel. *Les deux chercheurs sont en train d'appliquer et adapter leur modèle à la course des chevaux et envisagent de le mettre au service d'autres sports comme le patin à glace.
(5) Mots de W.H.Auden, essayaiste et critique, commentant la performance peu orthodoxe du coureur canadien Bruce Kidd, lui-même un athlète olympique, dans le court métrage « Runner » (1962).
